Historie fraktálu

Do doby, než byla objevena a popsána fraktální geometrie, byla euklidovská geometrie považována za nejsilnější nástroj popisu všech geometrických útvarů.

Euklidovská geometrie byla s úspěchem používána po celá staletí, avšak její slabinou, kterou si prakticky nikdo neuvědomoval, byl problém jak popsat jednoduchým způsobem složitě strukturované útvary. Tyto útvary mohly být jak matematického, tak i přírodního původu.

Běžné objekty jako úsečky, kruhy, čtverce, trojúhelníky, obdélníky, koule, krychle, jehlany lze poměrně snadno popsat pomocí euklidovské geometrie. Například pravoúhlý trojúhelník je plně popsán (každý jeho bod je jednoznačně určen) Pythagorovou větou.

Pokud by bylo třeba popsat jednoduchý fraktál jako je například Kochova křivka, pak by bylo nutné stanovit složitou a nepřehlednou rovnici. Tento objekt však může být jednoduše popsán pomocí fraktální geometrie.

Složitost Kochovy křivky lze dokonce popsat pomocí jednoho čísla, tzv. fraktální dimenze.

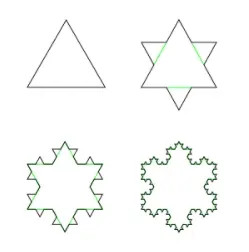
Kochova křivka

Označení fraktál tedy poprvé použil B. Mandelbrot. Ten je také označován za "otce" fraktální geometrie.

Je však pravdou, že matematické objekty dnes označované jako klasické fraktály (přesněji matematické deterministické fraktály), byly objeveny mnohem dříve, včetně Kochovy křivky.

Mandelbrot slovo "fraktál" použil pro všeobecné označení objektů, jejichž tvar je nezávislý na velikosti měřítka, pod kterým objekt pozorujeme.

Vyšel z významu latinského slova "fractus". Z něj odvozené slovo "frangere" znamená "rozlámat" - vytvořit nepravidelné úlomky.