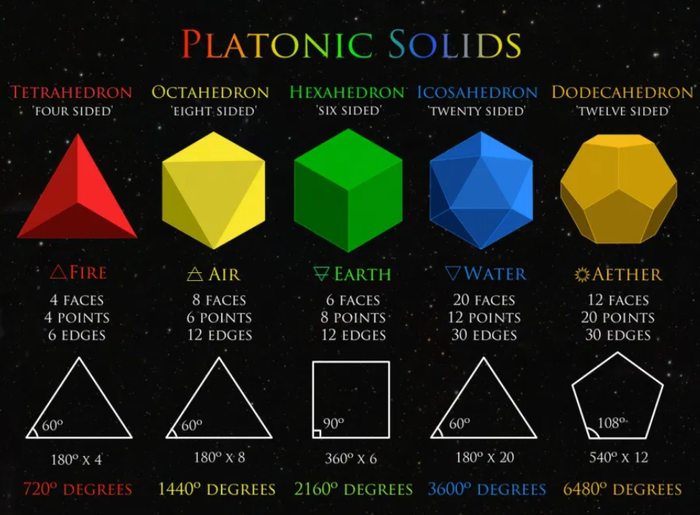
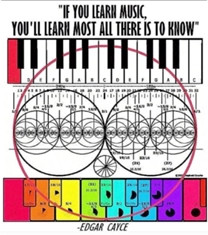
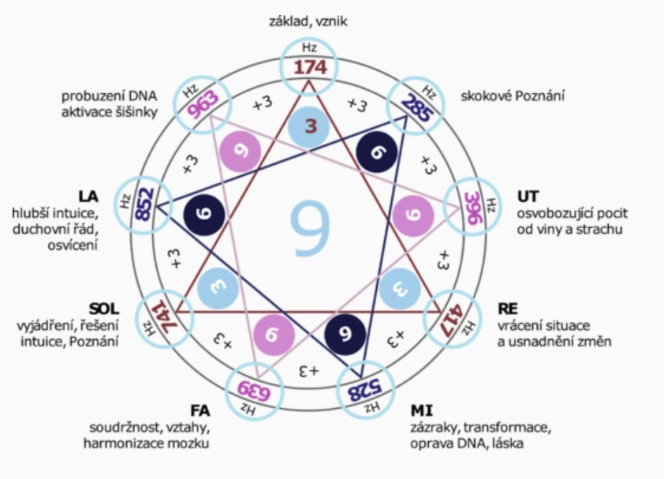
Oktáva
Z pohledu molekuly nebo vesmíru jsou čísla jen nuly a desetinné čárky, které vymezují různé rozsahy velikostí mezi perspektivami.
Je důležité si uvědomit, že přidání nul k číslu nemění jeho symboliku; pouze zvyšuje jeho velikost a posouvá ho na "vyšší sílu". Například 216 nese stejný základní význam jako 2 160, 21 600, 216 000 či 2 160 000.
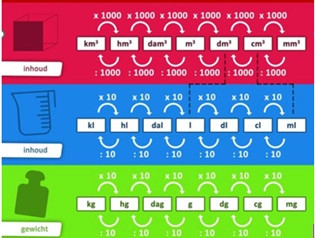
Toto souvisí s pojmy ze sanskrtského textu Satapatha Brahmana.
Sata znamená "více" nebo "mnoho" – násobky desítek, stovek či tisíců.
Patha odkazuje na mystický proces symbolizace, který umožňuje, aby jeden řád, úroveň či stav bytí byl vyjádřen různými způsoby.
Brahma je pak popisována jako nekonečná nesmírnost.

Pojďme se ponořit do jiné alternativy matematiky, která používá oktávy.
číslo 10 bylo považováno za první oktávu: 10: 1 + 0 = 1
číslo 20 bylo považováno za druhou oktávu: 20: 2 + 0 = 2
číslo 30 bylo považováno za třetí oktávu: 30: 3 + 0 = 3
číslo 28 se nachází ve třetí oktávě

Jak by vypadal náš matematický systém, kdybychom nuly a desetinné čárky nepoužívali?
Tento matematický jazyk využívá digitální kořeny a je známý jako vírová matematika.
Jejím cílem je najít nejmenší kořen čísla pouhým sečtením jeho číslic. Mnohé číselné sekvence tak mohou pokračovat donekonečna. Právě zde se objevují cykly, které se opakují stále dokola.

Mnozí lidé si myslí, že to není relevantní.
Tento model však odkrývá zcela nový obzor matematiky, který byl doposud skrytý našim očím. Je to, jako by vesmír ukazoval nový jazyk, nový způsob organizace.
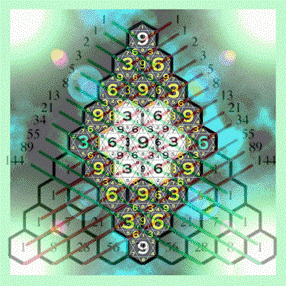
Tento způsob byl znám již ve starých přírodních vědách a je pravděpodobně používán i dnes, což dokazují symboly některých tajných organizací a světových elit. Tento postup se nazývá ciferace.

Ciferace (ciferný součet čísla) je pojem z aritmetiky, který označuje proces přiřazení každému přirozenému číslu jednociferného čísla vzniklého opakovaným sčítáním jeho číslic.

Je-li výsledek jednociferný, jedná se o ciferaci původního čísla.
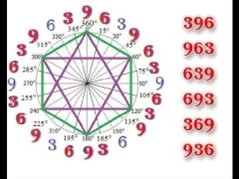
V opačném případě se opakuje sčítání cifer výsledku, dokud nedostaneme jednociferné číslo - ciferaci původního čísla.
Některé příklady využití ciferace (bude vysvětleno v dalších kapitolách).